Retargeting

The entire online marketing business is consumer obsessed. We dig into consumer activities, analyze their attributes, figure out their interests, in order to make use of every single bit of information to get engagement with consumers. Different components in the complex online marketing engine have their own purposes. Retargeting, the arguably most efficient short-term conversion optimization tool, is, in my opinion, all about business cycles.

Since the consumer fire the first pixel, the exploration has started and the new desire has been lit up. Massive marketing campaigns try to influence the consumers, while the consumers actively absorb information from various resources to help with the decision making. Our goal is to send the right messages to the right users at the right time. As we usually approach the problem from the campaign by campaign basis, the message needs to be sent is pre-defined. Two questions need to be answered are:

• Who are the right users?
• What is the right time?

The two questions are hardly separated. As time goes and purchase cycle changes, the users move on in their decision processes. That is to say, our ‘right users’ changes constantly. To better formulate the questions for the purpose of data analysis, I want to ask:

• In each defined period of time, who are the best users?

About timing

The answer to the above question comes from the data. The ultimate goal is to get the information about the business cycle without any human intervention. The starting time is defined as the last time the user hit any pixel in the funnel, including confirmation pixel and non-conformation pixel. Of course the nature of the pixel type carries a lot of information and would help further differentiate the users, and it will be incorporated in the model. We need to define the beginning of the business cycle in this manner, in order to make the best of the purchase pattern of a relatively small group of users to predict the vast majority. The engagement of the consumers is related to the time, in a complex manner. If we plot the potential of purchase over time, we would not expect to observe linear relationship, or quadratic curve, or any regular pattern we can describe simply.

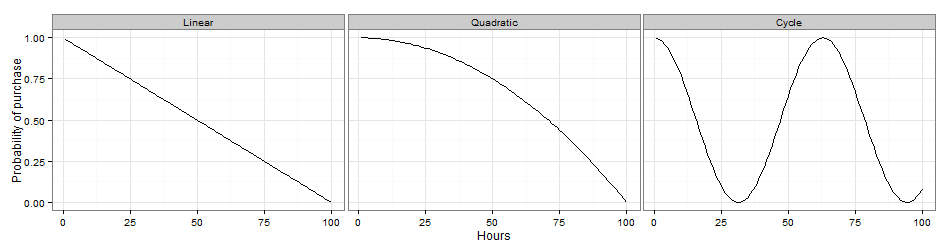
If we plot the observed probability of purchasing at each time point after the starting pixel, we are more likely to observe something like the following.

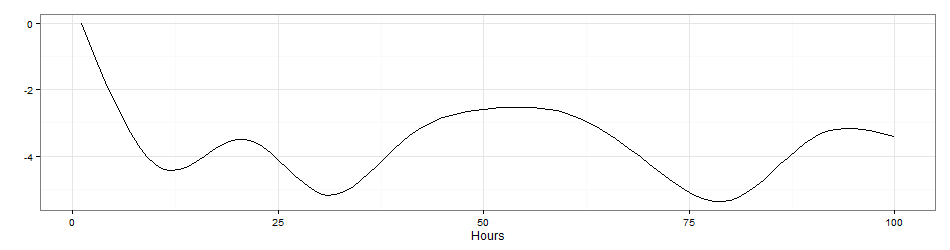
The proposed method is to expand the one dimensional time variable into a high dimensional non-parametric space. The high dimension allows us to make the best of the often limited purchase cases that only happened to a small group of consumers. Instead of guessing the pattern explicitly, increased volume in information allows using the computing resources to train the model and find out the most representative patterns. This ‘information expansion’ is achieved by extending the linear space in to a Reproducing Kernel Hilbert Space (RKHS). The real-valued funcitons inside RKHS is defined on a pre-defined domain, which, in cases of retargeting, is a bounded finite subset of real numbers. To find a finite representative basis of the RKHS, we resort to penalty terms. Fortunately, regularization theorems works nicely with RKHS.

The above Figure 2 used 10-Order Sobolev space basis.

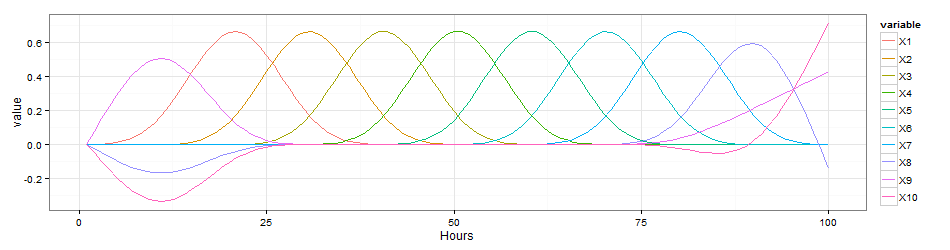
The sketchy outline is laid out, the details needs to be fill in. Two decisions need to be made before we can get a reasonably good representation of the purchase cycle,

• What Kernel do we use?
• What penalty term do we use?

In the very first version of the model, I used polynomial basis, which I believe is not the best choice after second thoughts. As I lost my previlage to try it out myself, here is a suggestion of different things to try:

• Basis:
  • natural cubic spline basis
  • Fourier basis

From the numerical stand point, all of these three basis are superior to the polynomial basis, as they all avoided to create extremely big numbers, which makes the parameter estimate much more stable.

• Penalty terms:
  • $L_1$ penalty
  • $L_2$ penalty

Here is a small simulation about the above ideas.

Subgroups of the audience

Of course we want to further differentiate the users. The frequent buyers and those who never bought anything should not be treated the same; those who make orders in the morning follow different purchase pattern comparing to those who make orders in the evening. To incorporate the user groups, we need to convert the sub-group information into categorical variables, and add the main effect and the interaction effect to the model.